Senior Experience Machine Learning Section 5 - Multiple Linear Regression

Multiple Linear Regression Intuition

Multiple linear regression depends on multiple independent variables, multiplied by coefficients

y = b₀ + b₁x₁ + b₂x₂+… b_n*x_n

Assumptions of a Linear Regression (for it to work good):	What it means:	So does my leaf dataset fit this?
Linearity	There must be a linear relationship between the outcome variable and the independent variables.	Yeah pretty much
Homoscedasticity	Random disturbance in the relationship are consistent	Not exactly, since the dataset is composed of 8 types of different leaf data, that creates non-randomness. But for each individual group though, the answer is pretty much yes.
Multivariate normality	Multiple regression assumes that the residuals (ypoint - yline) are normally distributed.
Independence of errors	Error must be random. The graph on the right has non-random error, while the graph on the left has random error.
Lack of multicollinearity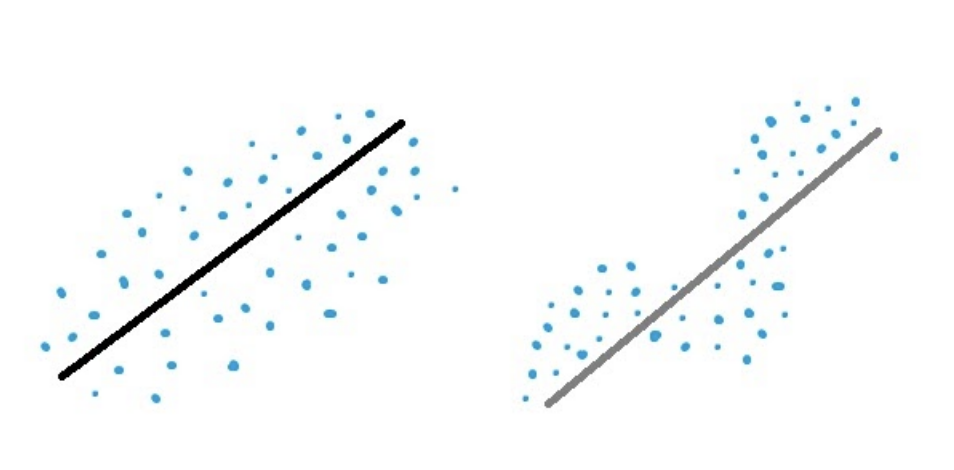

Dummy variables

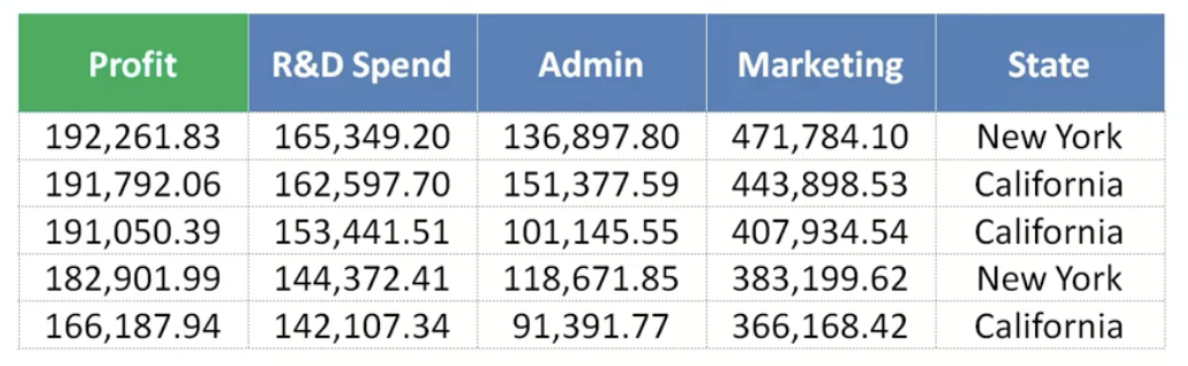
Profit - dependent variable

State column becomes dummy variables.

DUMMY VARIABLE:

NY	CA
1	0
0	1
0	1
1	0
0	1

y = b₀ + b₁x₁ + b₂x₂+… + b₄*D₁

Where b₀= a coefficient

Where b1 = r&d spent, b2 = admin, b3 = marketing, b4 = NY column, but don’t include CA column? This seems kinda sus, no info was lost but still doesn’t this value NY above CA or something

DUMMY VARIABLE TRAP:

y = b₀ + b₁x₁ + b₂x₂+… + b₄D₁ + b₅D₂

This is duplicating a variable, and can’t distinguish the different variables.

D₂ = 1 - D₁ creates an issue, it’s the same information…

This applies to any amount of dummy variables;

If you have 9 dummy variables, only put 8 in the equation

If you have 2, only include 1, etc.

P value - probability that the null hypothesis is correct

Building a Model

We don’t need to use every variable, some are unnecessary, add confusion to the data/results

1. Throwing in all your variables

2. Stepwise Regression

   1. Backwards Elimination (the fastest method out of these)

       1. Start with a significance level
      
       2. Throw in all the variables
      
       3. Remove the predictor variables with the highest P value above the significance level
      
       4. Refit Model, and remove predictors again
      
       5. Done.
      

   2. Forward Selection

       1. Start with a significance level
      
       2. Fit all simple regression models into the model, and select the one with the lowest P value and fit this variable into the model and keep going until none are below the significance level
      
       3. Done.
      

   3. Bidirectional Elimination

       1.  Start with significance levels, one to stay and one to enter the model
      
       2.  Perform <span style="text-decoration:underline;">forward selection</span>.
      
       3.  Perform all steps of the <span style="text-decoration:underline;">backwards elimination</span>, loop back to #2 until no new variables can enter and no old variables can exit the model
      
       4. Done.
      

3. Score Comparison (All Possible Models)

    1. Try straight up all 2^n-1 total combinations and choose the one with the best criterion of goodness, which needs to be preset.
   
    2. Done.
   

Tweet Post Link